1. 서 론
수중에 잠겨 있는 바닥 지형이 움직일 때 발생하는 파랑의 생성과 전파에 대해서는 과거부터 많은 연구가 수행되어 왔다. 특히 해저 지진에 의한 지진해일(Hammack, 1973; Wu, 1987; Lee et al., 1989; Tanioka and Satake, 1996; Dutykh and Dias, 2009; Lu et al., 2017a)이나 수중에서 물체가 움직이는 경우(Madsen and Hansen, 2012; Whittaker et al., 2017), 바닥이 주기적으로 움직이는 경우(Jung et al., 2018; Mahjouri et al., 2021; Jung et al., 2023) 등에 따른 파랑의 생성에 대한 연구들이 수행되었다. 본 연구에서는 이들 중 바닥이 주기적으로 움직이는 경우의 파랑 생성에 대한 해석적인 연구와 스펙트럼 법을 이용한 연구들에 중점을 두었다.
먼저 해석적인 방법으로는 Hammack(1973)이 연속방정식 및 자유수면 경계조건, 바닥 경계조건을 공간에 대해서는 Fourier 변환(Fourier transform), 시간에 대해서는 Laplace 변환(Laplace transform)하여 평평한 바닥이 수직으로 움직이는 경우 지진해일의 생성에 대해 선형의 해석해를 제시하였으며, 수리모형실험 결과와 비교를 통해 검증하였다. Dutykh et al.(2006)은 Hammack(1973)의 해를 3차원으로 확장하였으며, 지진해일의 생성과 전파에 대해 연구하였다. Lu et al.(2017a, 2017b)은 경사진 바닥이 움직이는 경우 지진해일의 생성 및 전파에 대해 선형의 해석해를 제시하였으며, Boussinesq 방정식을 이용한 비선형 수치해석 모델 및 수리모형실험 결과와 비교 검토하였다. Jung et al.(2018)은 Hammack(1973)과 동일한 기법을 적용하여 삼각형 형상의 바닥이 규칙적으로 움직이는 경우에 대한 해석해를 제시하였으며, 완경사방정식 결과와 비교를 통해 검증하였다. Jung et al.(2018)은 삼각형 형상의 바닥이 sine wave와 형상이 유사하기 때문에 바닥 조파장치의 형상으로 채택하였다. Jung and Son(2021)은 Hammack(1973)의 해석해를 이용하여 두 지점에서 시간 차이를 두고 바닥이 변형되는 경우 지진해일의 생성 및 전파특성에 대해 검토하였다. Mahjouri et al.(2021)은 고유함수전개법을 이용하여 삼각형 및 사각형 형상의 바닥이 규칙적으로 움직이는 경우 파랑 생성에 대한 선형의 2차원 해석해를 제시하였다. Jung and Lee(2022a)는 Jung et al.(2018)의 연구를 3차원 영역으로 확장하였으며, 바닥의 움직임을 이용하여 비스듬히 전파하는 파랑의 생성에 대한 선형의 해석해를 제시하였다. Jung et al.(2023)은 삼각형 및 사각형 형상의 바닥 움직임에 의한 선형파의 생성에 대한 해석해를 제시하였으며, 완경사방정식을 통해 결과를 검증하였다. 그들은 바닥 조파 장치를 이용한 불규칙파의 조파에도 성공하였다. 이처럼 최근에는 바닥의 움직임에 따른 지진해일에 대한 연구뿐만 아니라 실험실에서의 조파장치로 바닥의 움직임을 활용하려는 연구가 상당수 수행되었다.
수치해석적인 측면에서 스펙트럼법은 파랑변형 해석을 위한 비선형모형을 구축하는데 주로 사용되어 왔다. Zakharov(1968)는 Hamiltonian에 의해 결정되는 자유수면에서의 비선형 운동방정식을 유도하였다. Donmmermuth and Yue(1987)는 Zakharov(1968)의 방정식에 대해 고차 스펙트럼법을 이용하여 일정 수심에서 비선형 파랑을 해석할 수 있는 강비선형 모델을 제시하였다. 이들은 바닥의 움직임에 따른 파랑 생성에 대한 항들을 식에 포함하였지만 해석 결과는 제시하지 않았다. West et al.(1987)은 Donmmermuth and Yue(1987)와 유사한 방법을 이용하여 수심이 무한한 경우에 대한 강비선형 모델을 제시하였다. Craig and Sulem(1993)은 자유수면 위치에서 속도포텐셜과 수직방향 유속에 대한 관계를 정의하는 연산자(Dirichlet-Neumann operator)를 유도하고, 고차 스펙트럼법을 채택한 강비선형 모델을 제시하였다. Gyuenne and Nicholls(2007)는 Craig and Sulem(1993)의 연구에 수심의 변화에 따른 파랑변형을 모의할 수 있는 스펙트럼법을 제시하였다. 이들은 바닥의 움직임에 따른 파랑 변형을 고려할 수 있는 항들도 방정식에 포함시켰다. Klahn et al.(2020)은 비선형 파랑 변형 해석의 계산시간 단축을 위해 새로운 Implicit Taylor method를 제시하였다. 국내에서는 Jung(2023)이 바닥의 움직임에 따른 선형파 생성의 해석을 위한 단순화된 2차원 선형 스펙트럼 모델을 제시하였으며, 해석해와 비교하여 검증하였다.
본 연구에서는 Jung(2023)의 연구를 확장하여 바닥의 움직임에 따른 선형파 생성 해석을 위한 3차원 모델을 제시한다. Donmmermuth and Yue(1987)와 Gyuenne and Nicholls(2007)는 바닥 움직임에 따른 비선형파랑의 생성을 해석할 수 있는 강비선형 모델을 제시하였지만, 해석 결과는 논문에 제시하지 않거나 매우 단순한 경우에 대해서만 그 결과를 제시하였다. 또한 Gyuenne and Nicholls(2007)의 해석 결과는 2차원 공간에 국한되었다. 본 연구에서는 비록 선형모델이긴 하지만 다양한 형상의 바닥이 주기적으로 움직이는 경우의 파랑 생성을 모의할 수 있는 3차원 스펙트럼 모델을 제시한다. 본 스펙트럼 모델은 3차원적인 바닥 형상의 변화를 고려할 수 있고, 따라서 비스듬히 전파하는 파랑의 모의도 가능하다.
2. 바닥이 움직일 때 유체 영역에서 속도포텐셜
바닥이 움직일 때 유체영역에서 속도포텐셜은 연속방정식과 운동학적 바닥경계조건을 만족해야 한다. 해석을 위한 좌표 및 변수의 정의는 Fig. 1과 같다. 고정된 수심은 h0, 바닥의 움직임을 표현하는 함수는 η(x, y, t), 자유수면변위는 ζ(x, y, t)이다.
유체는 비압축성 및 비점성이며, 흐름은 비회전류로 가정하였다. 연속방정식과 바닥이 움직이는 경우 운동학적 바닥 경계조건은 다음과 같이 정의된다.
여기서, Φ는 속도포텐셜을 뜻한다. 위 식에서 비선형항을 제거하고 공간에 대해 Fourier 변환하면 다음 식과 같이 다시 쓸 수 있다.
여기서, m = k 1 2 + k 2 2
식(3)과 같은 연속방정식은 상미분방정식으로 다음과 같은 해를 갖는다.
여기서,
정수면에서의 속도포텐셜과 z 방향 속도포텐셜의 변화율은 식(8)을 이용하여 다음과 같이 나타낼 수 있다. 아래 식에서 A(k1, k2, t)는 미지수로 동역학적 및 운동학적 자유수면 경계 조건을 이용하여 결정할 수 있다.
3. 수치해석 기법
본 장에서는 바닥이 움직일 때 규칙파의 생성과 전파를 모의할 수 있는 선형 스펙트럼법에 대해 설명한다. Fourier 공간의 정수면에서 선형의 동역학적 및 운동학적 자유수면 경계조건은 다음 식과 같다(Jung, 2023). Zakharov(1968)에 의해 제시된 자유수면에서의 운동방정식도 비선형항을 제거하면 아래 식과 동일하다.
Donmmermuth and Yue(1987)와 Guyenne and Nicholls(2007)은 시간 적분을 수행할 때 4차 Runge-Kutta 법을 사용하여 해석하였으며, 수치해의 안정성이 확보됨을 보였다. Jung(2023)은 식(12) 및 (13)을 해석할 때 1차 정확도를 갖는 후방차분법(backward difference method)으로 시간미분항을 해석하였는데, 본 연구에서는 Donmmermuth and Yue(1987)와 Guyenne and Nicholls(2007)와 같이 4차 Runge-Kutta 법을 채택하여 수치모델의 정확도를 향상시켰다. 식(12)와 식(13)의 해석을 위해 아래 식들과 같이 4차 Runge-Kutta 법을 적용할 수 있다.
위의 식을 이용하여 수치해석을 수행할 때 각 시간 단계에서 ϕ ¯ W ¯ ϕ ¯ ζ ¯ W ¯
Jung(2023)이 후방차분법을 적용하여 시간미분항을 해석한 결과와 4차 Runge-Kutta 법을 적용한 결과를 x - z 2차원 공간에서 비교하였다. 수치해석 조건으로 수심(h0)은 1.0 m, 움직이는 바닥의 진폭(∆h0)은 0.1 m, 바닥의 폭(b)은 10.0 m이며, 바닥이 움직이는 주기(T)는 6.5초이다. 수치해석을 위한 계산시간 간격과 파수(wave number) 간격은 두 모델 모두 동일하게 각각 ∆t = T/1000 및 ∆k = π/500을 적용하였다. 움직이는 바닥의 형상은 삼각형 및 사각형 형상을 적용하였다. Jung(2023)의 결과와 본 연구의 결과는 Fig. 2에서 비교하였다. Fig. 2에서 symbol은 Jung et al.(2023)의 해석해이며, 파란색 파선은 Jung(2023)의 결과, 빨간색 실선은 본 연구의 결과이다. Fig. 2에서 수직축은 무차원 자유수면변위(ζ/∆h0)를 뜻하며, 수평축은 파장으로 무차원화한 움직이는 바닥(바닥 조파기)의 중앙으로부터 떨어진 거리(x/L)를 뜻한다. 본 시험 조건처럼 주기가 비교적 긴 경우 후방차분법을 적용한 Jung(2023)의 결과는 t = 5.0T 일 때, |x/L| > 2.5인 영역에서 약간의 오차가 발생하였으나, 본 연구의 결과는 해석해와 일치하는 결과를 보였다.
4. 움직이는 바닥에 대한 함수 정의 및 초기조건
4.1 삼각형 형상의 바닥이 snake 형상으로 움직이는 경우
3차원 공간에서 바닥이 움직일 때 파랑의 생성과 변형을 수치적으로 모의하기 위해서는 바닥의 움직임에 대한 함수 정의와 정수면에서의 속도포텐셜과 자유수면변위에 대한 초기조건이 필요하다. 4.1절에서는 x 축 방향으로 삼각형 형상이고, y 축 방향으로는 sine 함수 형상인 바닥이 y 축 방향으로 진행파 형태(snake 형상)로 움직이는 바닥에 대해 검토하였다(Fig. 3). 이와 같은 형상으로 움직일 경우 비스듬히 전파하는 파랑의 생성이 가능하다. 삼각형 형상의 바닥이 상하로 움직이는 진폭은 ∆h0, 움직이는 바닥의 x 방향 폭은 b1, 움직이는 바닥의 y 방향 길이는 b2로 정의하였으며, 이는 Fig. 3을 참고할 수 있다.
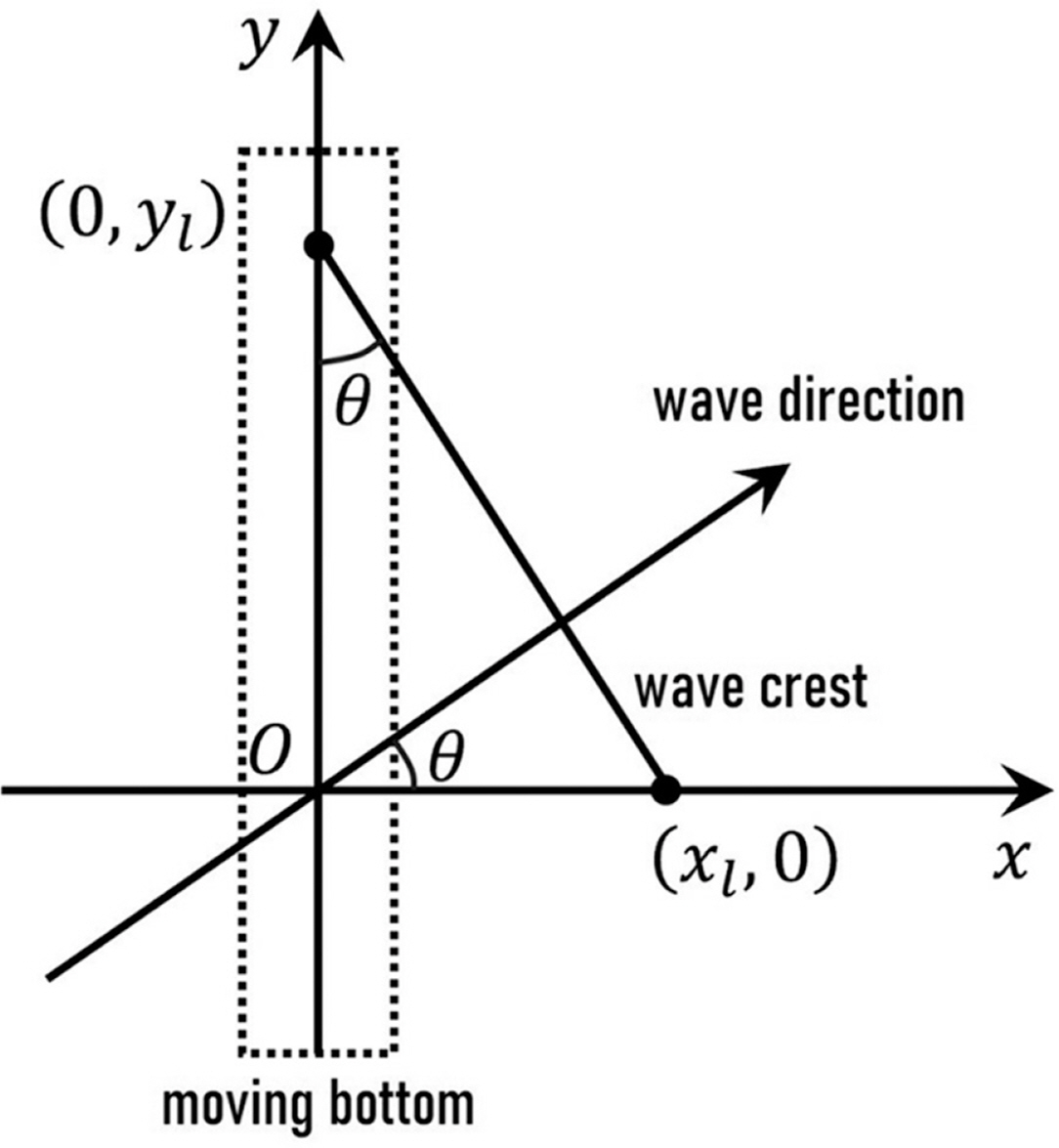
삼각형 형상의 바닥이 snake 형상으로 움직일 때 생성된 파랑은 비스듬히 전파한다. Fig. 4에서 xl은 ∆t초 동안 x 축을 따라 파랑의 파봉이 이동한 거리를 뜻하며, yl은 ∆t초 후에 파랑이 출발하는 y 값을 나타낸다. 이 때, y = yl인 지점에서 ∆t초 후의 위상은 y = 0인 지점에서 ∆t = 0일 때 위상과 같다.
따라서, 다음 식이 성립한다.
여기서, C는 파속(wave speed)을 의미하며, ω0는 움직이는 바닥의 각진동수(angular frequency)를 뜻한다. 그리고, θ는 파랑의 방향과 x 축 사이의 각도를 나타낸다. 식(21)에서 위상 변화율인 γ는 식(20)과 (21)로부터 다음과 같이 유도된다.
여기서, k0는 움직이는 바닥의 파수이며, 분산관계식 ω 0 2 = g k 0 tanh k 0 h 0 γ = - k 0 tan θ
바닥이 움직임에 따른 파랑 생성을 모의하기 위해서는 바닥의 형상과 움직임을 정의해야 한다. Fig. 3과 같은 형상의 바닥 움직임은 다음 식과 같이 정의된다.
식(23)은 x ≤ b 1 2
여기서,
여기서, H는 Heaviside step function을 뜻한다. 식(11)에서 α를 구하기 위해서는 η ¯ ∂ η ¯ ∂ t
여기서,
바닥이 움직이기 시작할 때(t = 0) 정수면에서의 속도포텐셜과 자유수면변위는 해석적으로 계산하여야 한다. 먼저 t = 0일 때, 정수면에서의 자유수면변위는 0임을 알 수 있다. t = 0일 때 속도포텐셜은 해석적으로 구할 수 있는데, Jung and Lee(2022a) 및 Jung and Lee(2022b)의 방법으로 구한 속도포텐셜의 해석해는 다음과 같다.
여기서,
따라서, 정수면(z = 0)에서 초기조건은 다음과 같이 정의된다.
4.2 사각형 형상의 바닥이 snake 형상으로 움직이는 경우
본 절에서는 3차원 공간에서 사각형 형상의 바닥이 snake 형상으로 움직이는 경우에 대한 함수 정의와 초기조건에 대해 검토하였다. 사각형 형상의 경우 바닥 조파장치로 제작이 용이한 형상이기 때문에 검토 조건에 포함하였다. 변수의 정의 및 바닥의 형상은 Fig. 5와 같다.
Fig. 5와 같은 사각형 형상의 바닥이 snake 형상으로 움직이는 상태를 정의하는 함수는 다음과 같이 정의된다.
5. 수치해석 결과
5.1 삼각형 형상의 바닥이 snake 형상으로 움직이는 경우
본 절에서는 삼각형 형상의 바닥이 snake 형상으로 움직이는 경우 파랑의 생성에 대해 검토하였다. 검토 조건으로 움직이는 바닥의 폭 b1 = L/4, 바닥의 길이 b2 = 5L로 설정하였다. 여기서, L은 주기적으로 움직이는 바닥에 의해 생성되는 파랑의 파장이다. 수심은 1.0 m, 움직이는 바닥의 진폭(∆h0)은 0.05 m이다. 3장에서 설명한 수치해석 기법으로 해석한 결과는 다음 식과 같은 Fourier 역변환을 통해 실제 공간에서 나타낼 수 있다. 식(44)는 고속 Fourier 역변환을 이용하여 계산하면 계산시간을 크게 단축할 수 있다.
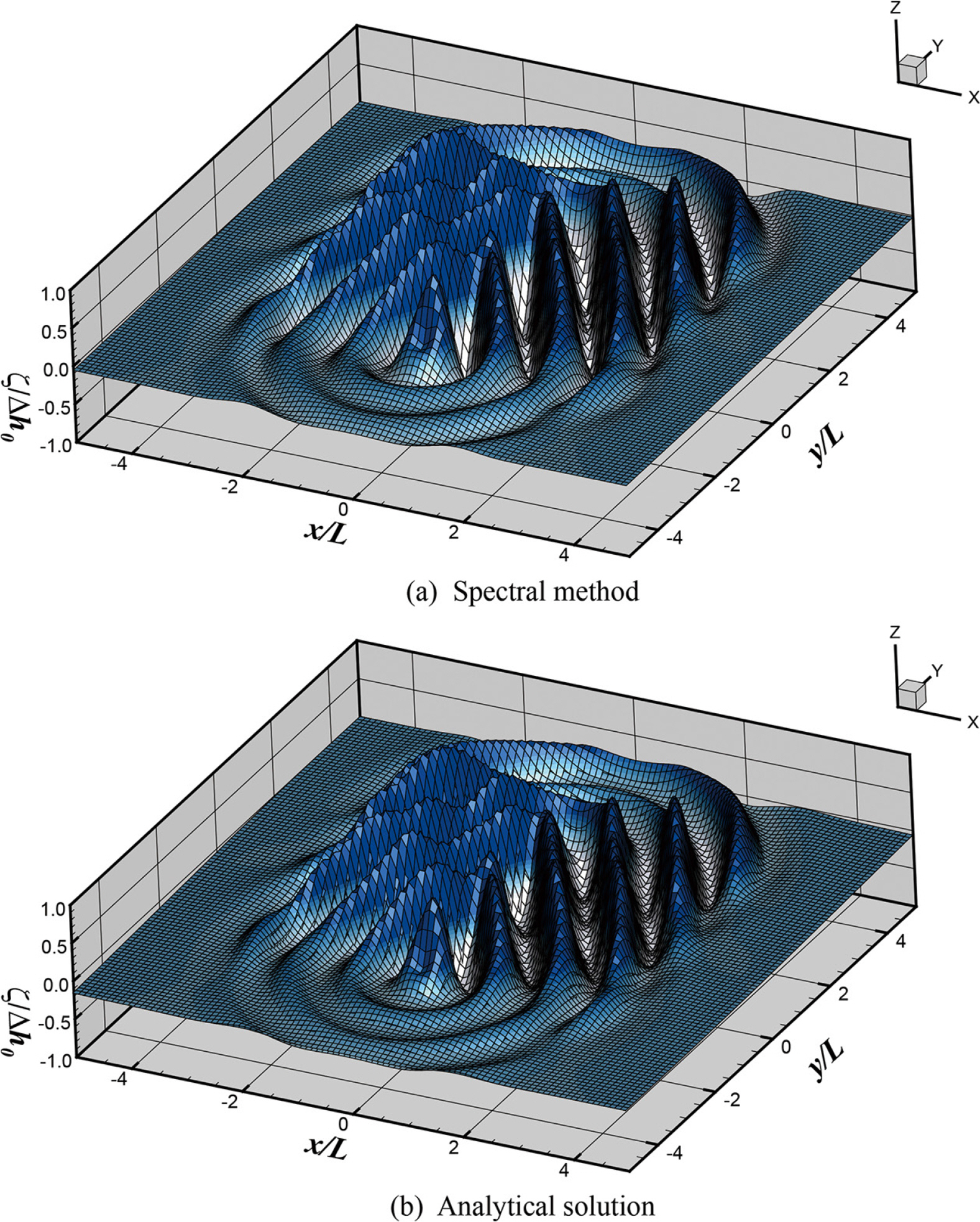
먼저 입사각이 0도인 경우(θ = 0)에 대해 검토하였다. 스펙트럼법을 이용한 수치해석 모델에서 ∆t = T/1000을 적용하였으며, ∆k1 = ∆k2 = π/500을 적용하였다. 수치해석 결과는 Fig. 6(a)에 나타내었으며, Jung and Lee(2022a)가 제시한 해석해의 결과는 Fig. 6(b)에 나타내었다. Fig. 6은 t = 4T인 시점의 결과이며, 수치해와 해석해는 거의 차이가 없이 동일한 결과를 보였다. 해석 조건은 x 축에 대한 파향이 0도인 경우로 전체적으로 동일한 높이의 바닥면이 z 축 방향으로 상하 운동하는 조건이며, 그림에서 x 축방향으로 평행하게 파랑이 전파하는 것을 볼 수 있다. 파봉을 따라 진동이 발생하는 현상은 파랑이 x 축 방향으로 전파하면서 y 축 방향으로 정온 한 영역 사이에 존재하는 에너지 불연속면에서 회절이 발생하기 때문이다. 이와 유사한 현상으로 Jung et al.(2021)이 반무한 방파제 주변 파랑의 파봉 및 파곡에서 진동이 발생하는 원인이 회절에 의한 것임을 설명하였다. 따라서, 실제 3차원 조파수조에서 바닥 조파장치를 이용하여 파랑을 조파할 때에는 회절 현상을 차단하기 위해 wave guide를 설치할 필요가 있다. Fig. 6(b)에 사용된 Jung and Lee(2022a)가 제시한 해석해는 다음 식과 같다.
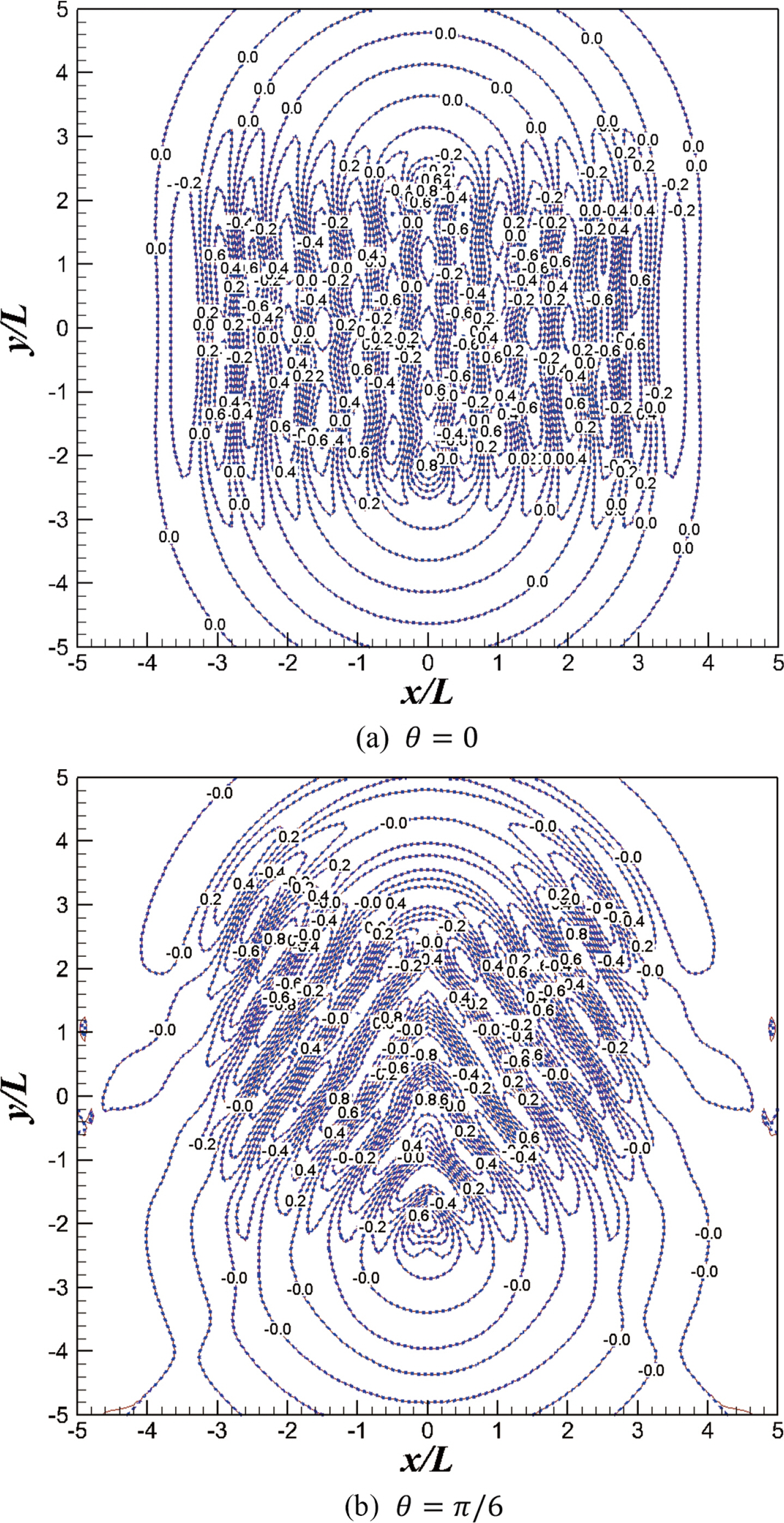
입사각이 30도인 경우(θ = π/6)에 대해 검토하였다. 스펙트럼법을 이용하여 수치해석한 결과는 Fig. 7(a)에 나타내었으며, Jung and Lee(2022a)가 제시한 해석해의 결과는 Fig. 7(b)에 나타내었다. Fig. 7에서 바닥이 snake 형식으로 움직임에 따라 비스듬히 전파하는 파랑이 생성된 것을 확인할 수 있으며, 수치해와 해석해는 거의 차이가 없이 동일한 결과를 보였다.
5.2 사각형 형상의 바닥이 snake 형상으로 움직이는 경우
본 절에서는 사각형 형상의 바닥이 snake 형상으로 움직이는 경우 파랑의 생성에 대해 검토하였다. 검토 조건은 삼각형 형상의 바닥이 움직이는 경우와 동일하며, 수치해석 모델의 조건 역시 동일하다. 사각형 형상의 바닥 움직임에 대한 해석해 또한 식(45) 및 (46)을 이용할 수 있으며, 형상함수 ∆ h 1 ¯ k 1 , k 2 ∆ h 2 ¯ k 1 , k 2
사각형 형상의 경우 삼각형 형상에 비해 바닥 움직임의 부피가 크기 때문에 생성되는 파랑의 진폭도 더욱 크게 나타났다(Figs. 9-10). 삼각형 형상의 바닥이 snake 형식으로 움직이는 경우와 마찬가지로 회절에 의해 파봉을 따라 진동이 발생하는 현상이 나타났다. 본 연구에서 제시한 스펙트럼법과 해석해의 결과는 거의 동일하게 나타났다.
Fig. 11에서 스펙트럼법에 의한 결과와 해석해에 의한 결과(무차원 자유수면변위)를 비교하였다. Fig. 8과 동일하게 실선은 해석해, 파선은 스펙트럼법에 의한 결과이며, 두 결과는 거의 일치함을 알 수 있다. 사각형 형상의 바닥이 움직일 때 생성된 파랑의 무차원 진폭(a/∆h0)은 입사각 0도일 때 최대 0.73356으로 계산되었으며, 이는 삼각형 형상의 바닥이 움직일 때 생성된 파랑의 진폭의 약 2배에 가깝다. 이와 같은 결과의 원인은 사각형 형상의 바닥 움직임의 부피가 삼각형 형상에 비해 2배 크기 때문인 것으로 생각된다.
해석해의 경우 바닥의 움직임이 함수 형태로 명확히 정의되는 경우에만 적용이 가능하다. 반면 본 연구에서 제시하는 스펙트럼법의 경우 임의의 바닥의 형상이나 움직임에 대해서도 해석이 가능하다. 특정 시간대에서 바닥의 변위(η)와 바닥 변위의 z 방향 변화율(∂η/∂z)을 알 수 있다면 이를 Fourier 변환하고, 식(9)에 대입하여 해석할 수 있다. 예를 들어, 불규칙한 형상의 단층에 의해 생성되는 지진해일이나, 수학적으로 정의가 어려운 형태의 인공구조물이 바닥에서 움직이는 경우 생성되는 파랑의 해석이 가능하다.
6. 결 론
본 연구에서는 3차원 공간에서 바닥의 움직임에 따른 파랑의 생성 및 전파를 해석할 수 있는 선형 스펙트럼법을 제시하였다. 연속방정식, 운동학적 바닥경계조건, 동역학적 및 운동학적 자유수면경계조건은 Fourier 공간에서 해석된다. 선형의 동역학적 및 운동학적 자유수면경계조건을 한 쌍의 지배방정식으로 채택하고, 시간에 대한 적분은 4차 Runge-Kutta법을 적용하여 해석하였다. 본 모델에서는 선형의 동역학적 및 운동학적 자유수면 경계조건을 이용하여 계산된 속도포텐셜이 연속방정식 및 운동학적 바닥경계조건을 항상 만족하도록 z 방향 속도포텐셜의 변화율(W ¯
먼저 x - z 2차원 공간에서 시간에 대한 적분을 4차 Runge-Kutta 법을 이용하여 해석한 결과가 Jung(2023)의 후방차분법을 이용한 결과보다 더욱 해석해와 일치하였다. 3차원 공간의 경우 삼각형 및 사각형 형상의 바닥이 snake 형식으로 규칙적으로 움직이는 경우에 대해 시험하였다. 본 연구에서 제시한 스펙트럼법을 사용하였을 경우, 바닥이 snake 형식으로 움직일 때 생성된 파랑이 비스듬히 전파하는 현상을 적절하게 재현하였다. 3차원 공간에서 시험한 결과, 본 연구의 스펙트럼법을 적용한 결과는 Jung and Lee(2022a)가 제시한 해석해와 거의 일치하는 결과를 보였다. 본 연구에서 제시한 스펙트럼법은 수식으로 정의할 수 있는 바닥 움직임에 대해서만 해를 제시할 수 있는 해석해와는 달리 바닥이 임의로 움직이는 경우에 대해서도 고속 Fourier 변환을 이용하여 해석이 가능하다는 장점이 있다.
본 연구에서는 3차원 공간에서 바닥의 움직임에 따른 파랑의 생성 및 전파를 해석할 수 있는 선형 스펙트럼법을 제시하였다. 일반적으로 파랑의 전파 해석에서는 비선형항을 모두 고려한 고차 펙트럼법이 제시되어 사용되고 있다. 따라서, 향후 3차원 공간에서 바닥의 움직임에 의한 비선형 파랑의 생성을 해석할 수 있는 고차 스펙트럼법에 대한 연구가 추가로 수행될 필요가 있을 것이다.